Fibonacci Series

Miss Preety Tailor

   

Fibonacci was a famous mathematician from Italy In 1202 he is working on population growth of rabbits.  It was the question of how fast rabbits could breed under ideal circumstances that Leonardo Fibonacci originally investigated in the year 1202.  Here was the question he posed:

Rabbit

Suppose a newborn pair of rabbits, one male and one female, is put in the wild. The rabbits mate at the age of one month and at the end of its second month a female can produce another pair of rabbits. Suppose that the rabbits never die and that each female always produces one new pair, with one male and one female, every month from the second month on.  How many pairs will there be in one year?

This can be represented in the following 'family tree' of rabbits:

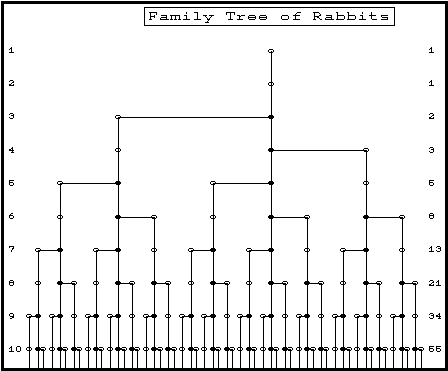
The column of numbers on the left shows the 'month', the column on the right shows the number of pairs of rabbits in that corresponding month.

He found that the number in each generation was always the sum of the number in the previous two generations. Hence, the series begins: 1, 1, 3, 5, 8, 13, 21, 34, 55, 89 ....

This series is known as Fibonacci series.

nth term of the series is given by

Fn = Fn-1 + Fn-2

Fibonacci Series In Nature

Fibonacci numbers appear every where in nature. The pattern by which seeds are arranged on a seed head is the same as that by which leaves are arranged around a stem, or petals around a flower.

For example, new cells are created only at the very tip (meristem) of a growing plant. They are formed in a spiral. This process of growth carries through all aspects of a plant's structure: 

Fibonacci numbers
in plant spirals

Fibonacci numbers
in plant branching

Fibonacci spirals in a sunflower seed

Fibonacci series in plant growth

Here a sunflower seed illustrates this principal as the number of clockwise spirals is 55 (marked in red, with every tenth one in white) and the number of counterclockwise spirals is 89 (marked in green, with every tenth one in white.)

Here a plant illustrates that each successive level of branches is often based on a progression through the Fibonacci series.

Why nature follows Fibonacci series?

This is no mere coincidence - it is 'natures way' of optimizing structures. Rotating by phi guarantees equal spacing of leaves and seeds no matter how far from the central starting point you go.

 

 

 

 

 

 

 

 

The above picture, showing the centre of a cone flower, illustrates that fact: notice how by one set rule the seeds are placed such that they are neither overcrowded in the middle nor sparse around the edges.

1. Leaves on stream are arranged in Fibonacci series so that it gets maximum possible exposure to light on each leaf.

2. Arranging them using Fibonacci series  the potential problem of the upper leaves overshadowing the lower ones, and also leaves the largest possible surface area open to catch rain water and direct it down the stem to the roots.
Take for example a pine cone. On examination it appears to be made up of patterns of spirals going in both directions. This is emphasized in colour. Interestingly, there are 13 anti-clockwise spirals (the pink ones) and 8 clockwise (in purple). This turns out to always be the case: the number of spirals going in both directions are consecutive terms in the Fibonacci series. This is just one example in which the numbers appear, and applies (though not always so visibly) to all natural growth. It is clearly evident, for example, in the picture of the coneflower at the top of this page.